Ortobicúpula cuadrada Enlaces externos Menú de navegación«Johnson Solid»
Sólidos de Johnson
geometríasólidos de Johnsoncúpulas cuadradasoctogonalesgirobicúpula cuadradaortobicúpulaprismarombicuboctaedrohexagonalbipirámide cuadrada elongadaoctaedroNorman Johnson
| Ortobicúpula cuadrada | ||
|---|---|---|
 Imagen del sólido | ||
| Tipo | Johnson J27 - J28 - J29 | |
| Caras | 8 triángulos 2+8 cuadrados | |
| Aristas | 32 | |
| Vértices | 16 | |
| Configuración de los vértices | 8(32.42) 8(3.43) | |
| Grupo de simetría | D4h | |
| Poliedro dual | - | |
| Propiedades | ||
convexo | ||
| Plano | ||
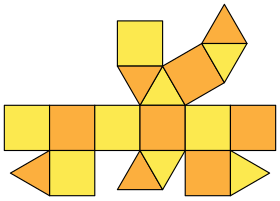 | ||
En geometría, la ortobicúpula cuadrada es uno de los sólidos de Johnson (J28). Como sugiere su nombre, puede construirse uniendo dos cúpulas cuadradas (J4) por sus bases octogonales, de forma que encajen caras similares entre sí. Al rotar una de las cúpulas 45-degree antes de unirla con la otra se obtiene una girobicúpula cuadrada (J29).
La ortobicúpula cuadrada es la segunda ortobicúpula de un conjunto infinito de ellas.
La ortobicúpula cuadrada puede elongarse mediante la inserción de un prisma octogonal entre sus dos cúpulas para formar un rombicuboctaedro, o se le puede quitar un prisma hexagonal irregular para formar una bipirámide cuadrada elongada (J15), que por sí sola es un octaedro elongado.
Los 92 sólidos de Johnson fueron nombrados y descritos por Norman Johnson en 1966.
Enlaces externos
Weisstein, Eric W. «Johnson Solid». En Weisstein, Eric W. MathWorld (en inglés). Wolfram Research.