Kdtyjb

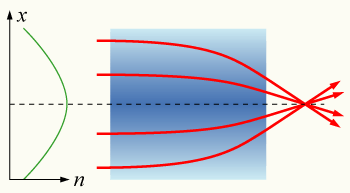
La óptica de gradiente de índice (disciplina también citada por su acrónimo en inglés, GRIN: Gradient-index) es la rama de óptica que cubre los efectos producidos por una variación gradual del índice de refracción de un material. Dichas variaciones se pueden usar para producir lentes con superficies planas, o lentes que no tienen los problemas de aberraciones típicos de las lentes esféricas tradicionales. Estas lentes pueden tener un gradiente de índice de refracción esférico, axial o radial.

En la naturaleza

El cristalino del ojo es el ejemplo más obvio de óptica de gradiente de la naturaleza. En el ojo humano, el índice de refracción de la lente varía desde aproximadamente 1,406 en las capas centrales, hasta 1,386 en las capas menos densas.^[1]​ Esto permite que el ojo muestre imágenes con buena resolución y baja aberración en distancias cortas y largas.^[2]​

Otro ejemplo de óptica de gradiente en la naturaleza son los espejismos, como las aparentes imágenes de charcos de agua que se pueden ver sobre las carreteras en los días calurosos. El efecto en realidad es provocado por una imagen del cielo, aparentemente ubicada sobre la carretera, debido a que los rayos de luz están siendo refractados (desviados) de su trayectoria recta normal. Esto se debe a la variación del índice de refracción entre el aire caliente menos denso en la superficie de la carretera y el aire frío más denso que se encuentra encima. La variación en la temperatura (y, por tanto, en la densidad) del aire provoca un gradiente en su índice de refracción, que aumenta con la altura.^[3]​ Este gradiente provoca la refracción de los rayos de luz del cielo, desviándolos hacia el ojo del espectador, de forma que su ubicación aparente coincide con la superficie de la carretera.

La atmósfera de la Tierra actúa como una lente con gradiente del índice de refracción, permitiendo a los observadores ver el sol durante unos minutos después de estar realmente debajo del horizonte, y que también puedan ver las estrellas situadas por debajo del horizonte.^[3]​ Este efecto también permite la observación de señales electromagnéticas de satélites después de que hayan descendido por debajo del horizonte, como en las mediciones de radio ocultación.

Aplicaciones

La capacidad de estas lentes para tener superficies planas simplifica el montaje de la lente, lo que las hace útiles donde muchas lentes muy pequeñas deben montarse juntas, como en los modelos de fotocopiadoras y escáneres. La superficie plana también permite que una lente de gradiente de índice se fusione fácilmente a una fibra óptica para producir una salida de luz colimada.

En aplicaciones de captación de imágenes, se utilizan principalmente para reducir las aberraciones. El diseño de tales lentes implica cálculos detallados de aberraciones, así como un proceso de fabricación eficiente. Se han utilizado varios materiales diferentes por sus propiedades, incluidos diversos plásticos y vidrios en cuya composición se incluye germanio, seleniuro de cinc y cloruro de sodio.

Ciertas fibras ópticas (fibras de índice graduado) están hechas con un perfil de índice de refracción variable radialmente; este diseño reduce fuertemente la dispersión refractiva de una fibra óptica multimodo. La variación radial en el índice de refracción permite una distribución de altura sinusoidal de los rayos de luz dentro de la fibra, evitando que los rayos salgan del núcleo. Esto difiere de las fibras ópticas tradicionales, que se basan en reflexión interna total. Las fibras de gradiente facilitan que todos los modos se propaguen a la misma velocidad, lo que permite un mayor ancho de banda temporal de la fibra.^[4]​

Los recubrimientos antirreflectantes son típicamente efectivos para rangos estrechos de frecuencia o ángulo de incidencia. Los materiales con índice gradual están menos restringidos en este sentido.^[5]​

Fabricación

Las lentes de gradiente de índice de refracción se fabrican mediante varias técnicas:

• Irradiación de neutrones: el cristal rico en Boro se bombardea con neutrones para provocar un cambio en la concentración de boro y, por lo tanto, del índice de refracción de la lente.^[6]​


• 
  Deposición química de vapor: implica el depósito de diferentes cristales con índices de refracción variables en una superficie para producir un cambio refractivo acumulativo.^[7]​


• 
  Polimerización parcial: un monómero orgánico se polimeriza parcialmente con radiación ultravioleta a intensidades variables para proporcionar un gradiente de refracción.^[8]​


• 
  Intercambio iónico: el vidrio se sumerge en una masa fundida líquida con iones de litio. Como resultado de de un proceso de difusión, los iones de sodio en el vidrio se intercambian parcialmente con los de litio, con una mayor cantidad de intercambio en el borde. Por lo tanto, la muestra adquiere una estructura de material progresivamente degradado, con el correspondiente gradiente del índice de refracción.^[9]​


• Rellenado de iones: la separación de fase de un vidrio específico hace que se formen los poros, que luego se pueden rellenar utilizando una variedad de sal o concentración de sales para dar un gradiente variable.^[10]​


• 
  Grabado láser directo: mientras se expone punto por punto la estructura previamente preparada, se varía la dosis de exposición (velocidad de escaneo y potencia del láser). Este proceso controla el grado de transformación de los monómeros a polímeros, y siendo espacialmente ajustable produce un índice de refracción variable. El método es aplicable a elementos microópticos de forma libre y óptica multicomponente.^[11]​

Historia

En 1854, James Clerk Maxwell sugirió una lente cuya distribución del índice de refracción permitiría obtener imágenes nítidas de cada región del espacio. Conocida como lente de Luneberg, implica una función de índice esférico y se espera que también tenga forma esférica. ^[12]​ (Maxwell, 1854). Sin embargo, esta lente es poco práctica y tiene poca utilidad, ya que solo los puntos en la superficie y dentro de la lente tienen una imagen nítida y los objetos extendidos sufren aberraciones extremas. En 1905, Robert Williams Wood utilizó una técnica de inmersión creando un cilindro de gelatina con un gradiente de índice de refracción que variaba simétricamente con la distancia radial desde el eje. Posteriormente se demostró que las rebanadas en forma de disco del cilindro tenían caras planas con distribución de índice radial. Demostró que, aunque las caras de la lente eran planas, actuaban como lentes convergentes y divergentes dependiendo de si el índice disminuía o aumentaba con respecto a la distancia radial.^[13]​ En 1964, se publicó un libro póstumo de Rudolf Luneburg, en el que se describía una lente de Luneberg que enfoca rayos de luz paralelos incidentes en un punto en la superficie opuesta de la lente.^[14]​ Esto también limita las aplicaciones de la lente porque es difícil de usar para enfocar la luz visible; sin embargo, tiene cierta utilidad en las aplicaciones de microondas.

Teoría

Una lente de índice de gradiente no homogénea posee un índice de refracción cuyo cambio sigue la función
n=f(x,y,z){displaystyle n=f(x,y,z)} según las coordenadas de la región de interés en el medio. De acuerdo con el principio de Fermat, la integral de trayectoria de luz (L), de un rayo luminoso que une dos puntos de un medio, es un proceso estacionario con respecto a su valor para cualquier curva cercana que une los dos puntos. La integral de la trayectoria luminosa viene dada por la ecuación

L=∫SoSnds{displaystyle L=int _{S_{o}}^{S}n,ds}, donde n es el índice de refracción y S es la longitud del arco de la curva. Si se usan coordenadas cartesianas, esta ecuación se modifica para incorporar el cambio en la longitud del arco para un gradiente esférico, a cada dimensión física:

L=∫SoSn(x,y,z)x′2+y′2+z′2ds{displaystyle L=int _{S_{o}}^{S}n(x,y,z){sqrt {x'^{2}+y'^{2}+z'^{2}}},ds}

donde los valores con comilla^[15]​ corresponden a d/ds. La integral de la trayectoria de la luz puede caracterizar su ruta a través de la lente de forma cualitativa, de modo que la lente pueda reproducirse fácilmente en el futuro.

El gradiente de índice de refracción de las lentes de gradiente de índice se pueden modelar matemáticamente de acuerdo con el método de producción utilizado. Por ejemplo, las lentes fabricadas de un material de índice de gradiente radial, como las Microlentes SELFOC,^[16]​ tienen un índice de refracción que varía de acuerdo con:

nr=no(1−Ar22){displaystyle n_{r}=n_{o}left(1-{frac {Ar^{2}}{2}}right)}, donde n_r es el índice de refracción a una distancia r del eje óptico; n_o es el índice de diseño en el eje óptico, y A es una constante positiva.

Referencias

Bibliografía

• Marchand, E W (1976). J. Opt. Soc. Amer. 66, 1326.