Kdtyjb

Corrimiento al rojo de las líneas espectrales en el espectro visible de un supercúmulo de galaxias distantes (derecha), comparado con el del Sol (izquierda). La longitud de onda se incrementa hacia el rojo y más allá.

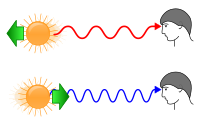
Corrimiento al rojo o al azul en función del movimiento relativo entre el objeto emisor y el observador.

Figura ilustrando el corrimiento al rojo de tipo gravitacional.

En física y astronomía, el corrimiento al rojo, acercamiento hacia el rojo o desplazamiento hacia el rojo (en inglés: redshift), ocurre cuando la radiación electromagnética, normalmente la luz visible, que se emite o refleja desde un objeto, es desplazada hacia el rojo al final del espectro electromagnético. De manera más general, el corrimiento al rojo es definido como un incremento en la longitud de onda de radiación electromagnética recibida por un detector comparado con la longitud de onda emitida por la fuente. Este incremento en la longitud de onda se corresponde con un decremento en la frecuencia de la radiación electromagnética. En cambio, el decrecimiento en la longitud de onda es llamado corrimiento al azul.
Cualquier incremento en la longitud de onda se llama "corrimiento hacia el rojo", incluso si ocurre en radiación electromagnética de longitudes de onda no visibles, como los rayos gamma, rayos X y radiación ultravioleta. Esta denominación puede ser confusa ya que a longitudes de onda mayores que el rojo (p.ej. infrarrojo, microondas y ondas de radio), los "desplazamientos hacia el rojo" se alejan de la longitud de onda del rojo. Así que al hablar de frecuencias de ondas menores que el rojo continua significando que la longitud de onda tiende a alargarse y no a asemejarse al rojo.

Un corrimiento hacia el rojo puede ocurrir cuando una fuente de luz se aleja de un observador, correspondiéndose a un desplazamiento Doppler que cambia la frecuencia percibida de las ondas sonoras. Aunque la observación de tales desplazamientos hacia el rojo, o su contrapuesto, hacia el azul, tiene numerosas aplicaciones terrestres (p.ej. Radar Doppler y pistola radar),^[1]​ la espectroscopia astronómica utiliza los corrimientos al rojo Doppler para determinar el movimiento de objetos astronómicos distantes.^[2]​ Este fenómeno fue predicho por primera vez y observado en el Siglo XIX cuando los científicos empezaron a considerar las implicaciones dinámicas de la naturaleza ondulatoria de la luz.

Otro mecanismo de corrimiento hacia el rojo es la expansión métrica del espacio, que explica la famosa observación de los corrimientos al rojo espectrales de galaxias distantes, quasares y nubes gaseosas intergalácticas se incrementan proporcionalmente con su distancia al observador. Este mecanismo es una característica clave del modelo del Big Bang de la cosmología física.^[3]​

Un tercer tipo de corrimiento al rojo, el corrimiento al rojo gravitacional (también conocido como efecto Einstein), es un resultado de la dilatación del tiempo que ocurre cerca de objetos masivos, de acuerdo con la relatividad general.^[4]​

Estos tres fenómenos, se pueden comprender bajo el paraguas de leyes de transformación de marcos. Existen otros muchos mecanismos con descripciones físicas y matemáticas muy diferentes que pueden conducir a un desplazamiento en la frecuencia de radiación electromagnética y cuyas acciones pueden ocasionalmente ser conocidas como "desplazamiento al rojo", incluyendo la dispersión y efectos ópticos.

Historia

La historia del corrimiento al rojo empezó con el desarrollo en el siglo XIX de la mecánica ondulatoria y la exploración del fenómeno asociado con el efecto Doppler. El efecto es llamado así después de que Christian Andreas Doppler ofreció la primera explicación física conocida para el fenómeno en 1842.^[5]​ La hipótesis fue probada y confirmada mediante ondas sonoras por el científico holandés Christophorus Buys Ballot en 1845.^[6]​ Doppler predijo correctamente que el fenómeno debería aplicarse a todas las ondas y en particular sugirió que la variación de los colores de las estrellas podía ser atribuida a su movimiento con respecto a la Tierra.^[7]​ Mientras que esta atribución terminó siendo incorrecta (los colores de las estrellas son indicadores de la temperatura, no del movimiento), Doppler sería posteriormente reivindicado por la verificación de observaciones de corrimiento al rojo.

El primer corrimiento al rojo Doppler fue descrito en 1848 por el físico francés Hippolyte Fizeau, que indicó que el desplazamiento en líneas espectrales visto en las estrellas era debido al efecto Doppler. El efecto es llamado algunas veces el "efecto Doppler-Fizeau". En 1868, el astrónomo británico William Huggins fue el primero en determinar la velocidad de una estrella alejándose de la Tierra mediante este método.^[8]​

En 1871, el corrimiento al rojo óptico fue confirmado cuando el fenómeno fue observado en las líneas de Fraunhofer utilizando la rotación solar, a unos 0.1 Å del rojo.^[9]​ En 1901 Aristarj Belopolsky verificó el corrimiento al rojo óptico en el laboratorio utilizando un sistema de rotación especular.^[10]​

La primera aparición del término "corrimiento al rojo" en la literatura, fue debida al astrónomo estadounidense Walter Sidney Adams en 1908, donde menciona "Dos métodos de investigación de la naturaleza del corrimiento al rojo nebular".^[11]​

Empezando con las observaciones en 1912, Vesto Slipher descubrió que muchas nebulosas espirales tenían considerables corrimientos al rojo.^[12]​ Posteriormente, Edwin Hubble descubrió una relación aproximada entre el desplazamiento al rojo de tales "nebulosas" (ahora conocidas como galaxias) y la distancia a ellas con la formulación de su epónimo la ley de Hubble.^[13]​ Estas observaciones corroboraron el trabajo de Alexander Friedman de 1922, en que halló las famosas ecuaciones de Friedmann, demostrando, que el Universo podía expandirse y presentó la velocidad de expansión en ese caso.^[14]​ Hoy son consideradas fuertes pruebas para un Universo en expansión y la Teoría del Big Bang.^[15]​

Medida, caracterización e interpretación

Un corrimiento al rojo se puede medir mirando el espectro de la luz que viene de una fuente sencilla. Si hay características en este espectro tales como líneas de absorción, líneas de emisión u otras variantes de intensidad de la luz, entonces en principio se puede calcular el corrimiento hacia el rojo. Para ello, se necesita la comparación del espectro observado con un espectro conocido de características similares. Por ejemplo, el hidrógeno, cuando está expuesto a la luz, tiene un espectro que muestra características a intervalos regulares. Si se observa el mismo patrón de intervalos en un espectro observado pero que ocurre a longitudes de onda desplazadas, entonces se puede medir el corrimiento al rojo del objeto. Para determinar el desplazamiento hacia el rojo de un objeto por tanto requiere un rango de frecuencias o longitudes de onda. Los desplazamientos al rojo no pueden ser calculados observando características sin identificar cuyas frecuencias residuales son desconocidas o con un espectro que no tiene características o ruido blanco (fluctuaciones aleatorias en un espectro.^[16]​

El corrimiento al rojo (y al azul) se pueden caracterizar por la diferencia relativa entre las longitudes de onda (o frecuencias) observadas y emitidas de un objeto. En astronomía, es habitual referirse a este cambio utilizando una magnitud adimensional llamada z. Si λ{displaystyle lambda } representa la longitud de onda f la frecuencia (λf=c{displaystyle lambda f=c} donde c es la velocidad de la luz, entonces z se define por las ecuaciones:

Medida del corrimiento al rojo, z{displaystyle z}

Basada en longitud de onda	Basada en frecuencia
z=λobservada−λemitidaλemitida{displaystyle z={frac {lambda _{mathrm {observada} }-lambda _{mathrm {emitida} }}{lambda _{mathrm {emitida} }}}}	z=femitida−fobservadafobservada{displaystyle z={frac {f_{mathrm {emitida} }-f_{mathrm {observada} }}{f_{mathrm {observada} }}}}
1+z=λobservadaλemitida{displaystyle 1+z={frac {lambda _{mathrm {observada} }}{lambda _{mathrm {emitida} }}}}	1+z=femitidafobservada{displaystyle 1+z={frac {f_{mathrm {emitida} }}{f_{mathrm {observada} }}}}

Después de medir z, la distinción entre el corrimiento al rojo y al azul es simplemente si z es positiva o negativa. Por ejemplo, en los corrimientos al azul (z < 0), el efecto Doppler está asociado con objetos aproximándose al observador en el que la luz se desplaza hacia energías mayores. Contrariamente, en los corrimientos al rojo (z > 0), el efecto Doppler está asociado a objetos alejándose del observador con la luz desplazándose hacia energías menores. Asimismo, los desplazamientos al azul del efecto Einstein están asociados con luz que entra en un fuerte campo gravitatorio mientras que los desplazamientos al rojo de efecto Einstein implican que la luz está dejando el campo.

Mecanismos

Un simple fotón propagado a través del vacío puede desplazarse hacia el rojo de varias maneras distintas. Cada uno de estos mecanismos produce un desplazamiento de tipo Doppler, es decir, z es independiente de la longitud de onda. Estos mecanismos son descritos mediante transformaciones galileanas, lorentzianas o relativistas entre un sistema de referencia y otro.^[2]​

Resumen de corrimientos al rojo

Tipo de corrimiento al rojo	Ley de transformación de sistema	Ejemplo de métrica	[17]​ Definición[18]​
Corrimiento al rojo Doppler	Transformaciones de Galileo	Distancia euclidiana	z=vc{displaystyle z={frac {v}{c}}}
Doppler relativista	Transformaciones de Lorentz	Métrica Minkowski	z=(1+vc)γ−1{displaystyle z=left(1+{frac {v}{c}}right)gamma -1}
Corrimiento al rojo cosmológico	Transformaciones relativistas	FLRW	z=anowathen−1{displaystyle z={frac {a_{mathrm {now} }}{a_{mathrm {then} }}}-1}
Corrimiento al rojo gravitacional	Transformaciones relativistas	Métrica de Schwarzschild	z=11−(2GMrc2)−1{displaystyle z={frac {1}{sqrt {1-left({frac {2GM}{rc^{2}}}right)}}}-1}

Efecto Doppler

Si una fuente de luz se está alejando de un observador, entonces ocurren los corrimientos al rojo (z > 0). Si la fuente se acerca, entonces ocurre un corrimiento al azul. Esto es válido para todas las ondas electromagnéticas y es explicado por el efecto Doppler. Consecuentemente, este tipo de corrimiento al rojo es denominado el corrimiento al rojo Doppler. Si la fuente se aleja del observador con velocidad v, entonces, ignorando los efectos relativistas, el corrimiento al rojo viene dado por

z≈vc{displaystyle zapprox {frac {v}{c}}}     (Ya que γ≈1{displaystyle gamma approx 1}, ver debajo)

donde c es la velocidad de la luz. En el efecto Doppler clásico, la frecuencia de la fuente no se modifica, pero el movimiento recesivo causa la ilusión de una frecuencia menor.

Efecto Doppler Relativista

Un tratamiento más completo del corrimiento al rojo Doppler necesita la consideración de efectos relativistas asociados con el movimiento de fuentes que se mueven con rapidez cercana a la velocidad de la luz. En breve, los objetos moviéndose cerca de la velocidad de la luz experimentarán desviaciones de la fórmula del efecto Doppler simple debido a la dilatación del tiempo de la relatividad especial que puede ser corregido introduciendo el factor de Lorentz γ{displaystyle gamma } en la fórmula clásica de Doppler como sigue:

1+z=(1+vc)γ{displaystyle 1+z=left(1+{frac {v}{c}}right)gamma }

Este fenómeno fue observado por primera vez en un experimento de 1938 realizado por Herbert E. Ives y G.R. Stilwell.^[19]​ Como el factor de Lorentz sólo depende de la magnitud de la velocidad, esto causa el desplazamiento hacia el rojo asociado con la corrección relativista para ser independiente de la orientación de la fuente del movimiento. En contraste, la parte clásica de la fórmula depende de la proyección del movimiento de la fuente en la línea de vista que proporciona diferentes resultados para diferentes orientaciones. Consecuentemente, para un objeto moviéndose formando un ángulo θ{displaystyle theta } con el observador (el ángulo nulo tiene una línea directa con el observador), la forma completa para el efecto Doppler relativista se convierte en:

1+z=1+vcos⁡(θ)/c1−v2/c2{displaystyle 1+z={frac {1+vcos(theta )/c}{sqrt {1-v^{2}/c^{2}}}}}

y solamente para los movimientos en la línea de vista (θ{displaystyle theta } = 0°, esta ecuación se reduce a:

1+z=1+vc1−vc{displaystyle 1+z={sqrt {frac {1+{frac {v}{c}}}{1-{frac {v}{c}}}}}}

Para el caso especial en que la fuente se está moviendo en ángulos rectos (θ{displaystyle theta } = 90°) al detector, el corrimiento al rojo relativista es conocido como el efecto Doppler transversal y un corrimiento al rojo de:

1+z=11−v2/c2{displaystyle 1+z={frac {1}{sqrt {1-v^{2}/c^{2}}}}}

es medido, incluso aunque el objeto no se está alejando del observador. Incluso si la fuente se está moviéndose hacia el observador, si hay un componente trensversal al movimiento entonces hay alguna velocidad a la que la dilatación cancela exactamente el corrimiento al azul esperado y a velocidades mayores la fuente que se aproxima se desplazaría hacia el rojo.^[20]​

Expansión del espacio

Galaxias con gran desplazamiento hacia el rojo del Campo Ultra Profundo del Hubble.

En la primera parte del siglo XX, Slipher, Hubble y otros hicieron las primeras medidas de corrimientos al rojo y al azul de galaxias más allá de la Vía Láctea. Inicialmente interpretaron estos desplazamientos al rojo y al azul como debidos únicamente al efecto Doppler, pero después Hubble descubrió una leve correlación entre el incremento del desplazamiento al rojo y el incremento de la distancia de galaxias. Los teóricos casi inmediatamente se dieron cuenta que estas observaciones se podían explicar por un mecanismo diferente de corrimiento al rojo. La ley de Hubble de la correlación entre corrimientos al rojo y distancias es requerida por los modelos de cosmología procedentes de la relatividad general que tienen una métrica de expansión del espacio.^[15]​ Como resultado, los fotones propagándose a través del Universo en expansión son extendidos, creando el corrimiento al rojo cosmológico. Esto difiere de los desplazamientos al rojo por efecto Doppler descritos antes porque la velocidad de empuje (p.ej. la transformación de Lorentz) entre la fuente y el observador no es debida a la transferencia clásica entre momento y energía, sino que en vez de ello los fotones incrementan su longitud de onda y se desplazan hacia el rojo según el espacio que están atravesando se expande.^[21]​ Este efecto está prescrito en el modelo cosmológico actual como una manifestación observable del factor de escala cósmico dependiente del tiempo (a{displaystyle a}) de la siguiente manera:

1+z=aahoraaentonces.{displaystyle 1+z={frac {a_{mathrm {ahora} }}{a_{mathrm {entonces} }}}.}

Este tipo de corrimiento al rojo se llama corrimiento al rojo cosmológico o corrimiento al rojo de Hubble. Si el Universo se estuviera contrayendo en vez de expandirse, veríamos las galaxias distantes desplazándose hacia el azul por una suma proporcional a su distancia en vez de desplazarse hacia el rojo.^[22]​

Estas galaxias no están retrocediendo simplemente por medio de una velocidad física alejándose del observador, en vez de ello, el espacio que interviene se está extendiendo, lo que cuenta lara la isotropía a gran escala del efecto demandado por el principio cosmológico.^[23]​ Para los desplazamientos al rojo cosmológicos con z < 0.1 los efectos de la expansión del espacio-tiempo son mínimos y los corrimientos al rojo están dominados por los movimientos relativos peculiares entre una galaxia a otra que causa corrimientos al rojo y al azul Doppler adicionales.^[24]​ La diferencia entre la velocidad física y la expansión del espacio se puede ilustrar por la Expansión de la Hoja de Caucho del Universo, una analogía cosmológica común utilizada para describir la expansión del espacio. Si dos objetos son representados por bolas de cojinetes y el espacio-tiempo por una hoja de caucho expandiéndose, el efecto Doppler es causado por el rodar de las bolas a través de la hoja creando un movimiento particular. El corrimiento al rojo cosmológico ocurre cuando las bolas de cojinetes se pegan a la hoja y la hoja es expandida. (Obviamente, hay problemas dimensionales con el modelo, ya que las bolas de cojinetes deberían estar en la hoja y el corrimiento al rojo produce velocidades mayores que las del efecto Doppler si la distancia entre dos objetos es lo suficientemente larga.).

A pesar de la distinción entre los corrimientos al rojo causados por la velocidad de los objetos y los asociados con la expansión del Universo, los astrónomos algunas veces lo llaman "velocidad de recesión" en el contexto de los desplazamientos al rojo de galaxias distantes a partir de la expansión del Universo, incluso aunque es sólo una recesión aparente.^[25]​ Como consecuencia, la literatura popular a menudo utiliza la expresión "corrimiento al rojo Doppler" en vez de "corrimiento al rojo cosmológico" para describir el movimiento de las galaxias dominado por la expansión del espacio, a pesar del hecho de que una "velocidad cosmológica recesiva" cuando se calcula no igualará la velocidad en la ecuación de Doppler relativista.^[26]​ En particular, el corrimiento al rojo Doppler está acotado por la relatividad especial; con lo que v > c es imposible mientras, en contraste, v > c es posible para corrimientos al rojo cosmológicos porque el espacio que separa los objetos (p.ej. un cuásar desde la tierra) se puede expandir más deprisa que la velocidad de la luz.^[27]​ Más matemáticamente, el punto de vista de que "las galaxias distantes están retrocediendo" y el punto de vista de que "el espacio entre galaxias está expandiéndose" está relacionado con el cambio de sistema de coordenadas. Expresando de forma precisa requiere trabajar con las matemáticas de la métrica de Friedman-Lemaître-Robertson-Walker.^[28]​

Derivación matemática

Las consecuencias observacionales de este efecto pueden ser deducidas usando las ecuaciones de la relatividad general que describen un universo homogéneo e isotrópo. Para obtener la expresión del corrimiento al rojo, se parte de la ecuación de una geodésica para una onda luminosa, que es:

ds2=0=−c2dt2+a2dr21−kr2{displaystyle ds^{2}=0=-c^{2}dt^{2}+{a^{2}dr^{2} over 1-kr^{2}}}

donde

• 
  ds2{displaystyle ds^{2}} es el intervalo espacio-tiempo


• 
  dt2{displaystyle dt^{2}} es el intervalo de tiempo


• 
  dr2{displaystyle dr^{2}} es el intervalo espacial


• 
  c es la velocidad de la luz


• 
  a es factor de escala, dependiente del tiempo cósmico


• 
  k es la curvatura gaussiana

Para un observador que observa la cresta de una onda luminosa en una posición r=0{displaystyle r=0} y en un tiempo t = tahora{displaystyle t_{mathrm {ahora} }}, la cresta de la onda luminosa fue emitida en t = tentonces{displaystyle t_{mathrm {entonces} }} en el pasado y desde una posición distante r=R{displaystyle r=R}. La integración sobre la trayectoria tanto en el espacio como en el tiempo sobre la que viaja la onda luminosa proporciona:

c∫tentoncestahoradta=∫R0dr1−kr2{displaystyle cint _{t_{mathrm {entonces} }}^{t_{mathrm {ahora} }}{frac {dt}{a}};=int _{R}^{0}{frac {dr}{sqrt {1-kr^{2}}}},}

En general, la longitud de onda de luz no es la misma en las dos posiciones y tiempos contemplados debido a las características cambiantes de la métrica. Cuando la onda fue emitida, esta tenía una longitud de onda λentonces{displaystyle lambda _{mathrm {entonces} }}. La siguiente cresta de la onda luminosa fue emitida en un tiempo:

t=tentonces+λentonces/c{displaystyle t=t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c,}

El observador ve que la siguiente cresta de la onda luminosa observada, con una longitud de onda λahora{displaystyle lambda _{mathrm {ahora} }} le llega en un tiempo:

t=tahora+λahora/c{displaystyle t=t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c,}

Desde esta cresta posterior ha sido también emitida desde r=R{displaystyle r=R}, y se observa en r=0{displaystyle r=0}, se puede escribir la siguiente ecuación:

c∫tentonces+λentonces/ctahora+λahora/cdta=∫R0dr1−kr2{displaystyle cint _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}};=int _{R}^{0}{frac {dr}{sqrt {1-kr^{2}}}},}

El lado derecho de las dos ecuaciones integrales de arriba son idénticos, por lo tanto:

c∫tentonces+λentonces/ctahora+λahora/cdta=c∫tentoncestahoradta{displaystyle cint _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}};=cint _{t_{mathrm {entonces} }}^{t_{mathrm {ahora} }}{frac {dt}{a}},}

Operando:

0=∫tentoncestahoradta−∫tentonces+λentonces/ctahora+λahora/cdta=∫tentoncestentonces+λentonces/cdta+∫tentonces+λentonces/ctahoradta−∫tentonces+λentonces/ctahora+λahora/cdta=∫tentoncestentonces+λentonces/cdta−(∫tnowtentonces+λentonces/cdta+∫tentonces+λentonces/ctahora+λahora/cdta)=∫tentoncestentonces+λentonces/cdta−∫tahoratahora+λahora/cdta{displaystyle {begin{aligned}0&=int _{t_{mathrm {entonces} }}^{t_{mathrm {ahora} }}{frac {dt}{a}}-int _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}}\&=int _{t_{mathrm {entonces} }}^{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{frac {dt}{a}}+int _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }}{frac {dt}{a}}-int _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}}\&=int _{t_{mathrm {entonces} }}^{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{frac {dt}{a}}-left(int _{t_{mathrm {now} }}^{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{frac {dt}{a}}+int _{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}}right)\&=int _{t_{mathrm {entonces} }}^{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{frac {dt}{a}}-int _{t_{mathrm {ahora} }}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}}end{aligned}}}

Finalmente se obtiene

∫tahoratahora+λahora/cdta=∫tentoncestentonces+λentonces/cdta{displaystyle int _{t_{mathrm {ahora} }}^{t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{frac {dt}{a}};=int _{t_{mathrm {entonces} }}^{t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{frac {dt}{a}},}

Para muy pequeñas variaciones en el tiempo (como lo es un período de una onda luminosa) el factor de escala es esencialmente un constante (a=aahora{displaystyle a=a_{mathrm {ahora} }} y a=aantes{displaystyle a=a_{mathrm {antes} }}). Esto permite simplificar las integrales:

tahora+λahora/caahora−tahoraaahora=tentonces+λentonces/caentonces−tentoncesaentonces{displaystyle {frac {t_{mathrm {ahora} }+lambda _{mathrm {ahora} }/c}{a_{mathrm {ahora} }}}-{frac {t_{mathrm {ahora} }}{a_{mathrm {ahora} }}};={frac {t_{mathrm {entonces} }+lambda _{mathrm {entonces} }/c}{a_{mathrm {entonces} }}}-{frac {t_{mathrm {entonces} }}{a_{mathrm {entonces} }}}}

que se puede rescribir como

λahoraλentonces=aahoraaentonces{displaystyle {frac {lambda _{mathrm {ahora} }}{lambda _{mathrm {entonces} }}}={frac {a_{mathrm {ahora} }}{a_{mathrm {entonces} }}},}

Usando la definición de corrimiento al rojo proporcionado más arriba, se obtiene la expresión del corrimiento al rojo cosmológico en función del factor de escala que se estaba buscando:

1+z=aahoraaentonces{displaystyle 1+z={frac {a_{mathrm {ahora} }}{a_{mathrm {entonces} }}}}

En un universo como el que habitamos que se expande, el factor de escala aumenta monótonamente con el tiempo, así, z es positivo y las galaxias distantes aparecen con corrimiento al rojo. Usando un modelo de la expansión del Universo, el corrimiento al rojo se puede relacionar con la edad de un objeto observado, llamada relación tiempo cósmico–corrimiento al rojo. Dada una relación de densidad como Ω0{displaystyle Omega _{0}}:

Ω0=ρρcrit ,{displaystyle Omega _{0}={frac {rho }{rho _{text{crit}}}} ,}

Donde ρcrit{displaystyle rho _{text{crit}}} es la densidad crítica del universo en expansión.^[29]​ A grandes corrimientos al rojo se encuentra que:

t(z)=23H0Ω01/2(1+z)3/2 ,{displaystyle t(z)={frac {2}{3H_{0}{Omega _{0}}^{1/2}(1+z)^{3/2}}} ,}

Donde H0{displaystyle H_{0}} es la constante de Hubble actual, y z es el corrimiento al rojo.^[30]​

Corrimiento al rojo gravitacional

En la teoría de la relatividad general, existe la dilatación temporal dentro de pozos gravitacionales. Esto se conoce como el corrimiento al rojo gravitacional o desplazamiento Einstein.^[31]​ La demostración teórica de este efecto se obtiene del la solución de Schwarzschild de las ecuaciones de Einstein, de las que se puede obtener el desplazamiento al rojo asociado a un fotón que viaja a través del campo gravitatorio generado por una masa esféricamente simétrica, sin carga eléctrica y no rotatoria:

1+z=11−(2GMrc2){displaystyle 1+z={frac {1}{sqrt {1-left({frac {2GM}{rc^{2}}}right)}}}},

donde

• 
  G{displaystyle G,} es la constante gravitacional,


• 
  M{displaystyle M,} es la masa del objeto que crea el campo gravitatorio,


• 
  r{displaystyle r,} es la coordenada radial del observador (que es análoga a la distancia clásica desde el centro del objeto, pero realmente es una coordenada Schwarzschild, y


• 
  c{displaystyle c,} es la velocidad de la luz.

Este desplazamiento al rojo gravitacional se puede calcular a partir de la suposición de la relatividad especial y el principio de equivalencia; la teoría de la relatividad general al completo no es necesaria.^[32]​

El efecto es muy pequeño pero medible en la Tierra utilizando el efecto Mossbauer, y fue observado por primera vez en el experimento de Pound y Rebka.^[33]​ Sin embargo, es significativo cerca de un agujero negro, y cuando un objeto se aproxima al horizonte de sucesos el desplazamiento al rojo tiende a infinito. Es también la causa dominante de las grandes fluctuaciones de temperatura de escala angular en el fondo cósmico de microondas (ver el efecto Sachs-Wolfe).^[34]​

Observaciones astronómicas

El corrimiento al rojo observado en astronomía se puede medir porque los espectros de emisión y absorción para átomos son distintivos, calibrados a partir de los experimentos de espectroscopia en laboratorios terrestres. Cuando el corrimiento al rojo de varias líneas de absorción y emisión desde un simple objeto astronómico es medida, z se encuentra que es extraordinariamente constante. Aunque los objetos distantes pueden estar ligeramente borrosos y las líneas ensanchadas, no es más que porque se puede explicar por los movimientos térmicos y mecánicos de la fuente. Por estas y otras razones, el consenso entre los astrónomos es que los desplazamientos al rojo que observan son debidos a alguna combinación de estas tres formas establecidas de desplazamientos al rojo estilo Doppler. Las hipótesis alternativas no son consideradas generalmente como plausibles.^[35]​

La espectroscopia, como medida, es considerablemente más difícil que la simple fotometría, que mide el brillo de objetos astronómicos a través de filtros.^[36]​ Cuando los datos fotométricos son los únicos disponibles (por ejemplo, en el Campo Profundo del Hubble y el Campo Ultra Profundo del Hubble), los astrónomos confían en una técnica de medida de desplazamientos al rojo fotométricos.^[37]​ Debido a la sensibilidad del filtrado en un rango de longitudes de onda y la técnica que confía en muchas suposiciones sobre la naturaleza del espectro en una fuente de luz, los errores para estos tipos de medida pueden estar en rangos superiores a z = 0.5 y son muchos menos fiables que las resoluciones espectroscópicas.^[38]​ Sin embargo, la fotometría permite al menos una caracterización cualitativa de un corrimiento al rojo. Por ejemplo, si un espectro tipo solar tiene un corrimiento al rojo de z = 1, sería más brillante en los infrarrojos que en el color amarillo-verde asociado con el pico de su espectro de cuerpo negro y la intensidad de la luz se reducirá en el filtro en un factos de dos (1 +z) (ver la corrección K para más detalles en las consecuencias fotométricas del corrimiento al rojo).^[39]​

Observaciones locales

En objetos cercanos (dentro de nuestra Vía Láctea), los desplazamientos al rojo observados están casi siempre relacionados con las velocidades de la LOS asociadas con los objetos que están siendo observados. Las observaciones de tales desplazamentos al rojo y al azul han permitido a los astrónomos medir velocidades y parametrizar las masas de las órbitas estelares en binarias espectroscópicas, un método empleado por primera vez en 1868 por el astrónomo británico William Huggins.^[8]​ De forma similar, los pequeños desplazamientos al rojo y al azul detectados en las medidas espectroscópicas de estrellas individuales son una manera de que los astrónomos puedan diagnosticar medir la presencia y características de sistemas planetarios alrededor de otras estrellas.^[40]​ Las medidas de desplazamientos al rojo para detalles finos se utilizan en heliosismología para determinar los movimientos precisos de la fotosfera del Sol.^[41]​ Los desplazamientos al rojo también se han utilizado para hacer las primeras medidas de la rotación de los planetas,^[42]​ velocidades de nubes interestelares,^[43]​ la rotación de galaxias,^[2]​ y la dinámica del disco de acrecimiento en estrellas de neutrones y agujeros negros que exhiben desplazamientos al rojo Doppler y gravitacionales.^[44]​ Adicionalmente, las temperaturas de emisión y absorción de varios objetos se puede obtener midiendo el ensanchamiento Doppler, los desplazamientos al rojo y al azul sobre una línea sencilla de absorción o emisión.^[45]​ Midiendo el ensanchamiento y los desplazamientos de 21-centímetros de la línea del hidrógeno en diferentes direcciones, los astrónomos han podido medir las velocidades de recesión de gas interestelar, que al final reveló la curva de rotación de nuestra Vía Láctea.^[2]​ Se han realizado medidas similares en otras galaxias, como la de Andrómeda.^[2]​ Como herramienta de diagnóstico, las medidas de desplazamiento al rojo son una de las más importantes medidas espectoscópicas hechas en la astronomía.

Observaciones extragalácticas

Los objetos más distantes exhiben los mayores corrimientos al rojo correspondientes al flujo de Hubble del Universo. Los mayores desplazamientos observados, correspondientes a las mayores distancias y a los más lejanos atrás en el tiempo, son los de la Radiación cósmica de microondas y el valor numérico de su desplazamiento, según las mejores medidas que se disponen actualmente, que son las publicadas por la Colaboración Planck en 2018, es aproximadamente z = 1089.8 (z = 0 se corresponde al momento actual) y muestra el estado del Universo hace unos 13787 millones de años y 372000 años después de los momentos iniciales del Big Bang.^[46]​

Los núcleos luminosos puntuales de los quasars fueron los primeros objetos "altamente-desplazados al rojo"(z>0.1{displaystyle z>0.1}) descubiertos antes de que la mejora de los telescopios permitiera el descubrimiento de otras galaxias altamente desplazadas. Actualmente, el corrimiento al rojo de quasar medidos más alto es de z=6.4{displaystyle z=6.4},^[47]​ con la confirmación de que el mayor corrimiento al rojo de una galaxia es z=7.0{displaystyle z=7.0}^[48]​ mientras que otros informes no confirmados más de una lente gravitacional observada en un cúmulo de galaxias distante puede indicar que una galaxia tiene un desplazamiento al rojo de z=10{displaystyle z=10}.^[49]​

Para galaxias más lejanas del Grupo Local y cercanas al Cúmulo de Virgo, pero dentro de unos miles de megaparsecs, el corrimiento al rojo es aproximadamente proporcional a la distancia de la galaxia. Esta correlación fue observada por Edwin Hubble y es conocida como la ley de Hubble. Vesto Slipher fue el descubridor de los corrimientos al rojo galáctico. En torno al año 1912, mientras Hubble correlaba las medidas de Slipher con las distancias las midió por otros medios para formular su Ley. En el modelo ampliamente aceptado basado en la relatividad general, los desplazamientos al rojo es sobre todo un resultado de la expansión del espacio: esto significa que el más allá de una galaxia es desde nosotros, la mayoría del espacio se ha expandido en el tiempo desde que la luz dejó la galaxia, así que la mayoría de la luz se ha extendido, la mayoría de la luz se ha desplazado al rojo y así pacece que se está moviendo desde nosotros. La ley de Hubble viene en parte del principio copernicano.^[23]​ Como no se conoce normalmente cómo de luminosos son los objetos, la medición del corrimiento al rojo es más fácil que las medidas de distancia más directas, de tal manera que los corrimientos al rojo son algunas veces convertidos en una medida de distancia utilizando la ley de Hubble.

Las interacciones gravitatorias de las galaxias las unas con las otras y con los cúmulos causan una dispersión en el dibujo normal del diagrama de Hubble. Las velocidades peculiares asociadas con galaxias superpuestas dejando un rastro rudo de masa de objetos virializados en el Universo. Este efecto conduce a tal fenómeno como en las galaxias cercanas (como la galaxia de Andrómeda) exhibiendo desplazamientos al azul según caemos hacia un baricentro común y los mapas de corrimientos al rojo de cúmulos muestran un efecto de Dedo de Dios debido a la dispersión de velocidades peculiares en una distribución esférica.^[23]​ Este componente añadido da a los cosmólogos una oportunidad de medir las masas de objetos independientes de la relación masa-luz (la relación de la masa de una galaxia en masas solares con su brillo en luminosidades solares), una herramienta importante para medir materia oscura.^[50]​

La relación lineal de la ley de Hubble entre la distancia y el corrimiento al rojo asume que la tasa de expansión del Universo es constante. Sin embargo, cuando el Universo era mucho más joven, la tasa de expansión y entonces la "constante" de Hubble era mayor que en la actualidad. Para galaxias más distantes, cuya luz ha estado viajando durante mucho más tiempo, la aproximación de la tasa de expansión constante falla y la ley de Hubble se convierte en una relación integral no lineal y dependiente de la historia de la tasa de la expansión ya que la emisión de luz desde la galaxia en cuestión. Las observaciones de la relación de distancia del corrimiento al rojo se puede utilizar, entonces, para determinar la historia de expansión del Universo y así la materia y energía contenida.

Durante mucho tiempo se creyó que la tasa de expansión había estado continuamente decreciendo desde el Big Bang, observaciones recientes de la relación de distancia de corrimiento al rojo utilizando supernovas tipo Ia han sugerido que en tiempos comparativamente recientes el Universo ha empezado a acelerarse.

El corrimiento al rojo en expediciones

Con la aparición de los telescopios automatizados y las mejoras en los espectroscopios, se han realizado varias colaboraciones para mapear el Universo en el corrimiento al rojo del espacio. Combinando estos desplazamientos al rojo con datos de posiciones angulares, una expedición de corrimiento al rojo mapea la distribución 3D de materia dentro de una parte del cielo. Estas observaciones suelen medir propiedades de la estructura a gran escala del universo. La Gran Muralla, un gran supercúmulo de galaxias a unos 500 millones de años luz, proporciona un ejemplo dramático de una estructura a gran escala que las expediciones de corrimiento al rojo pueden detectar.^[51]​

La primera expedición de corrimiento al rojo fue la CfA Redshift Survey, que empezó en 1977 y completó la colección de datos inicial en 1982.^[52]​ Más recientemente, la 2dF Galaxy Redshift Survey halló la estructura a gran escala de una sección del Universo, midiendo valores de z de más de 220000 galaxias, la recolección de datos se completó en 2002 y el conjunto final de datos se lanzó el 30 de junio de 2003.^[53]​ (Además de los patrones de mapeo a gran escala de galaxias, el 2dF estableció un límite superior para la masa del neutrino). Otra expedición notable, el Sloan Digital Sky Survey (SDSS), sigue su curso (al menos en 2005) e intenta obtener medidas de unos 100 millones de objetos.^[54]​ El SDSS ha grabado corrimientos al rojo para galaxias por encima de 0.4 y se ha involucrado en la detección de quasars más allá de z = 6. La DEEP2 Redshift Survey utiliza los telescopios Keck con el nuevo espectrógrafo "DEIMOS]]. Una continuación del programa piloto DEEP1, DEEP2 está diseñado para medir galaxias débiles con desplazamientos al rojo de 0.7 y superiores y está por tanto planeado para complementar al SDSS y al 2dF.^[55]​

Desplazamientos hacia el rojo más altos

Gráfico de distancia (en giga años luz) vs. desplazamiento hacia el rojo según el Modelo Lambda-CDM.

Los objetos con los mayores desplazamientos al rojo son las galaxias y las ráfagas de rayos gamma. Las muestras más confiables provienenten de análisis espectrales, el desplazamiento hacia el rojo confirmado como el más alto es el de la galaxia GN-z11, con z=11.1, es decir, 400 millones de años después del Big Bang.^[56]​ El objeto que anteriormente era considerado con mayor desplazamiento hacia el rojo es la galaxia UDFy-38135539, con un valor de z=8.6.^[57]​ El brote de rayos gamma más distante es el GRB 090423, descubierto en abril de 2009, tiene un corrimiento hacia el rojo de z=8.2.^[58]​ Mientras que ULAS J1342+0928 es el cuásar conocido más lejano, con un valor de z=7.54.^[59]​ La radio galaxia más lejana es TN J0924-2201 y tiene un desplazamiento de z=5.2.^[60]​ El material molecular más alejado conocido es una emisión de CO desde el cuásar SDSS J1148 + 5251, con un desplazamiento hacia el rojo de z=6.42.^[61]​

Los objetos extremadamente rojos (ERO) son fuentes astronómicas de radiación que emiten energía en la parte roja e infrarroja del espectro electromagnético. Como las galaxias de alta tasa de formación de estrellas, o las galaxias elípticas con una población estelar más antigua.^[62]​ Según las últimas medidas publicadas por la Colaboración Planck en 2018, a la radiación de fondo de microondas le corresponde un desplazamiento hacia el rojo de z=1089.8, es decir, nació unos 372,000 años después del Big Bang, y la distancia actual a la superficie de último esparcimiento es de más de 45 mil millones de años luz. En junio de 2015 se informó que estrellas de galaxias emisoras de radiación Lyman-alfa indican valores de z=6.60.^[63]​ Es probable que dichas estrellas existieron en un universo muy temprano y comenzaron la creación de elementos químicos más pesados que el hidrógeno, que son necesarios para la formación de planetas y cualquier tipo de vida.^[64]​

Efectos debidos a transferencias ópticas o radiactivas

Las interacciones y fenómenos resumidos en las materias de transferencia radiactiva y óptica física pueden dar como resultado desplazamiendos en la longitud de onda y la frecuencia de la radiación electromagnética. En tales casos los desplazamientos se corresponden a una transferencia física de energía a materia u otros fotones más que debida a una transformación entre marcos de referencia. Estos desplazamientos pueden ser debidos a tales fenómenos físicos como el efecto Wolf o la dispersión de radiación electromagnética desde partículas elementales cargadas, desde partículas o desde fluctuaciones del índice de refracción en un medio dieléctrico como ocurre en el fenómeno de los radio silbidos.^[2]​ Mientras tales fenómenos son conocidos como "corrimientos al rojo" y "corrimientos al azul", las interacciones físicas de los campos de radiación electromagnética con materia propia o intermedia distingue estos fenómenos de los efectos de marcos de referencia. En astrofísica, las interacciones de materia ligera que proporcionan desplazamientos de energía en el campo de radiación son generalmente conocidos como "enrojecidos" más que "desplazados al rojo", que como término, normalmente está reservado para los mecanismos discutidos anteriormente.^[2]​

En muchas circunstancias la dispersión causa que la radiación se enrojezca porque la entropía resulta de la predominancia de muchos fotones de baja energía sobre unos cuantos de alta energía (cumpliendo el principio de conservación de la energía).^[2]​ Excepto posiblemente bajo condiciones cuidadosamente controladas, la dispersión no produce el mismo cambio relativo en la longitud de onda a través de todo el espectro; es decir, cualquier z calculada es generalmente una función de la longitud de onda. Más allá, la dispersión de materia aleatoria generalmente ocurre en muchos ángulos y z es función del ángulo de dispersión. Si ocurre la dispersión múltiple o las partículas dispersadas tienen movilidad relativa, entonces generalmente también se produce distorsión de línea espectral.^[2]​

En astronomía interestelar, el espectro visible puede aparecer enrojecido debido a procesos de dispersión en un fenómeno conocido como enrojecimiento interestelar.^[2]​ De forma similar la dispersión de Rayleigh causa el enrojecimiento atmosférico del Sol visto en el amanecer o el ocaso y causa que el resto del cielo tenga un color azul. Este fenómeno es distinto del desplazamiento al rojo porque las líneas espectroscópicas no están desplazadas a otras longitudes de onda en objetos enrojecidos y hay un oscurecimiento adicional y una distorsión asociada con el fenómeno debido a los fotones que son dispersados dentro y fuera de la LOS.

Véase también

• Efecto Doppler

Referencias

Notas

Artículos

• Odenwald, S. & Fienberg, RT. 1993; "Reconsideraciones de Corrimientos al Rojo de Galaxias" en Sky & Telescope Feb. 2003; pp31-35 (Este artículo es una útil lectura en la que se distinguen 3 tipos de corrimiento al rojo y sus causas).


• Lineweaver, Charles H. y Tamara M. Davis, "Ideas equivocadas sobre el Big Bang", Scientific American, marzo de 2005. (Este artículo es útil para explicar el mecanismo de corrimiento al rojo cosmológico así como aclarar equívocos reapecto a la física de la expansión del espacio).


• Bedran, M.L.(2002)"A comparison between the Doppler and cosmological redshifts" Am. J. Physics 70(4), 406-408. http://www.df.uba.ar/users/sgil/physics_paper_doc/papers_phys/cosmo/doppler_redshift.pdf
  

Referencias de libros

• 
  Binney, James; Michael Merrifeld (1998). Princeton University Press, ed. Astronomía Galáctica. ISBN 0-691-02565-7. 
  


• 
  Carroll, Bradley W. y Dale A. Ostlie (1996). Addison-Wesley Publishing Company, Inc., ed. Una Introducciñin a la Astrofísica Moderna. ISBN 0-201-54730-9. 
  


• 
  Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). Addison-Wesley, ed. Lecturas de Feynman sobre Física Vol. 1. ISBN 0-201-51003-0. 
  


• 
  Kutner, Marc (2003). Cambridge University Press, ed. Astronomía: Una Perspectiva Física. ISBN 0-521-52927-1. 
  


• 
  Misner, Charles; Thorne, Kip S. and Wheeler, John Archibald (1973). W. H. Freeman, ed. Gravitación. San Francisco. ISBN 0-7167-0344-0.  La referencia utiliza el parámetro obsoleto |coautores= (ayuda)
  


• 
  Peebles, P. J. E. (1993). Princeton University Press, ed. Principios de Cosmología Física. ISBN 0-691-01933-9. 
  


• 
  Taylor, Edwin F.; Wheeler, John Archibald (1992). W.H. Freeman, ed. Física espacio-temporal: Introducción a la Relatividad Especial (2º ed.). ISBN 0-7167-2327-1. 
  


• 
  Weinberg, Steven (1971). John Wiley, ed. Gravitación y Cosmología. ISBN 0-471-92567-5. 
  

Enlaces externos

• 
  Wikimedia Commons alberga una galería multimedia sobre Corrimiento al rojo.


• Corrimiento al rojo gravitacional


• Tutorial de Cosmología de Ned Wright


• Artículo sobre al corrimiento al rojo en SPACE.com


• Guía de referencia cósmica sobre desplazamientos al rojo


• Tutorial Astronómico de Mike Luciuk sobre Corrimientos al Rojo

En español:

• Las galaxias de alto corrimiento al rojo


• El efecto Doppler y el corrimiento al rojo de los espectros estelares.


• Desplazamientos al rojo


• Desplazamiento al rojo cosmológico


• Vídeo de Hubblecast que explica el corrimiento al rojo mediante las imágenes de Campo Ultra-profundo del Hubble